A while back I was looking at the different maximum values that the different integer data types (uint8, short, int, long, etc) have throughout a couple languages I’ve been using and noticed that none of them ended in zero. I wondered why that was but then relatively quickly realized that it is because integer data types in computers are made up of bytes and bits.
An 8-bit (1-byte) integer has a max value of  , a 16-bit (2-byte) integer has a max value of
, a 16-bit (2-byte) integer has a max value of , etc. In fact since any integer in a computer is made of bits it will have a maximum value of
, etc. In fact since any integer in a computer is made of bits it will have a maximum value of 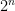 . The prime factorization of an n-bit integer is in the notation, it is n 2s all multiplied together. Like so:
. The prime factorization of an n-bit integer is in the notation, it is n 2s all multiplied together. Like so: 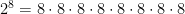
In order for something to end in a zero it must be a multiple of 10, and the prime factorization of 10 is 5 * 2, and the prime factorization of 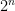 will never contain a 5. Case closed. That was fun.
will never contain a 5. Case closed. That was fun.
That got me thinking about figuring out how many zeroes are at the end of a number if all you have is the prime factorization. Using my basic arithmetic skills I found out that:
It appears (although isn’t proof) that the lowest quantity between twos and fives dictates how many zeroes are at the end of a number when you’re looking at its prime factorization. I tried this with many more combinations and it worked with every one of them.
So what can we do with this information?
A factorial is a number written as  where for any value
where for any value  ,
,  . For example
. For example  and
and  . The Wikipedia page for factorials shows that
. The Wikipedia page for factorials shows that 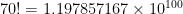 . That’s a big number, over a googol. You can see the whole thing here on WolframAlpha.
. That’s a big number, over a googol. You can see the whole thing here on WolframAlpha.
Continue reading Factorizeroes! →